Mathematical Calculators
Probability Calculator
The probability calculator lets you explore the relationships of likelihood between two separate events. This allows you to get a better understanding of how events are related, and thereby makes predictions more accurate.
Probabilities of single events
%
%
Which probability do you want to see?
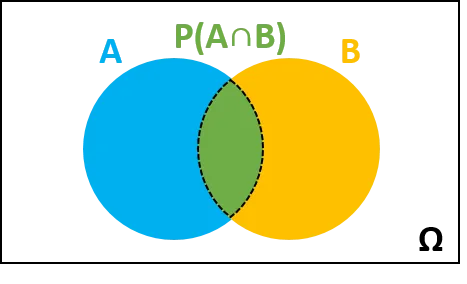
%
Probabilities for a series of events
times
%
Table of contents
| ◦Probability definition |
| ◦Conditional probability |
| ◦Theoretical vs experimental probability |
| ◦Probability and statistics |
The probability calculator is a helpful tool when investigating the relationships between events, such as the chance of A happening and the chance of B happening. For example, if the chance of A happening is 50%, and the same for B, what are the chances of both happening, only one happening, at least one happening, or neither happening, and so on?
Our probability calculator helps you see the probability of six different scenarios. Plus, when you enter in how many times the "die is cast", it provides you with four more scenarios. This way, you don't have to do all the calculation yourself. Just type in the numbers and our calculator will take care of the rest!
Understanding Probability: Definition and Concept
Conditional Probability: Dependent and Independent Events
Theoretical vs Experimental Probability
Using the Probability Calculator: Inputs and Outputs
Probability and Statistics: Real-Life Applications
Common Mistakes to Avoid when Calculating Probability
Additional Resources and Further Reading
Conclusion: How the Probability Calculator Can Help You Make Better Decisions
Probability definition
Probability is a way of thinking about uncertain situations and is used in a variety of fields, such as gambling, decision making, and statistics. The definition of probability given in this course is the most basic and fundamental definition of the subject.
Conditional probability
Probability is all about studying chance, and one of the most important concepts to understand is whether events are dependent or not. Two events are independent if the occurrence of the first one doesn't affect the likelihood of the occurrence of the second one. This is incredibly important, because it determines how we can calculate potential outcomes. If we roll a perfectly balanced standard cubic die, there's a 1/6 chance of getting a two.
Even though the dice have been linked together in this example, the probability of getting a two ⚁ in the second turn is still 1/6 because the events are independent. This means that the probability of getting at least one particular result, like a two ⚁ in the first turn, does not depend on what happens to the dice in the second turn.
In probability, there are different ways of looking at a scenario. This time, we're going to talk about conditional probability. Suppose you're playing a game of tennis and one of your opponents approaches the net. Depending on the angle at which they hit the ball, it may be possible to send the ball past their opponent in one shot. However, if their opponent ducks when they see the ball coming, the ball will likely bounce off the ground and their opponent might catch it. This is an example of a situation where thinking about the game in terms of events (hitting the ball) and outcomes.
Theoretical vs experimental probability
In most cases, theoretical probability is defined as the ratio between the number of favorable outcomes to the number of every possible outcome. However, there is a difference between theoretical probability and experimental probability. The formal definition of experimental probability is the ratio between the number of outcomes that fall under a specific category (the experiment) to the total number of outcomes. Experimental design relies on the given information, logical reasoning, and telling us what to expect from the experiment. Ideally, this information will come from the hypothesis being tested. After gathering this information, the experimental design will help you design the experiment in a way that will validate or invalidate your hypothesis.
In the game of 42 marbles, one ball is randomly picked and put back in the bag for an infinite number of times. This means that there are always 42 balls in the bag, 18 of which are orange. We can calculate the probability of picking a particular color by dividing the number of balls of that color by the total number of balls in the bag (42). This is simplified to 3/7, or the probability is 18/42, which means that out of every 14 balls picked, there should be 3 orange balls.
Probability is a mathematical science which deals with the chance of something happening. It can be used to predict what will happen as a result of performing an experiment, or to understand the odds of something happening in a given situation. In this example, we'll be using the experimental probability to understand what happened when we picked a marble from a bag and repeated the procedure 13 more times. Suppose we got 8 orange balls in 14 trials. This gives us the empirical probability of 8 out of 14, or 44%.
There will be times when you will pick more cards, times when you will get less, and times when you will pick the predicted number. The outcome, however, will differ from the theoretical one. This happens because when you try to reiterate this game over and over, sometimes, you will pick more, and sometimes you will get less, and sometimes you will pick exactly the number predicted theoretically. If you sum up all results, you should notice that the overall probability gets closer and closer to the theoretical probability. If not, then there may be a discrepancy between what you are seeing and the hypothetical outcome - this could be the case, for example, if some balls in the bag are of different colors and sizes. In order to get an accurate estimate, you will need to randomize the selection process.
Probability and statistics
Statistics is the branch of mathematics that deals with the collection, interpretation, analysis, presentation, and interpretation of data. Probability is the branch of mathematics that studies the possibility of events, and its outcomes. It is important to understand these differences, as they can lead to different conclusions in different situations.
Probability is a theoretical field of math that deals with things such as mathematical definitions and theorems. In contrast, statistics is a practical application of math that tries to attribute sense and understanding of observations in the real world. Statistics can be divided into two main branches - descriptive and inferential. Descriptive statistics examines the descriptive properties of a population, such as counts, means, and standard deviations. Inferential statistics uses statistical methods to draw conclusions about a population from samples, either from a experiment or from observations taken from the real world.
Probability is the ability to predict the possibility of events, while statistics is the study of the frequency of past occurrences. By the end of the course, you will have a deeper understanding of these concepts, and be able to use them to model real-world data.
Suppose you are playing a game of chance, where each card is chosen with the same probability, and your goal is to win. In this case, you could make a bet based on the odds - that is, the probability that your chosen card will be a spade. Assuming that the deck is complete and the choice is entirely random and equitable, you could deduce that the probability is equal to ¼. This means that you can confidently make a bet.
A statistician will watch the game for a while to assess the fairness before consulting with the probabilist on what actions to take to have the best chance of winning. After they agree that playing the game is worth it, the probabilist will advise what steps to take to improve their chances.
Article author
John Cruz
John is a PhD student with a passion to mathematics and education. In his freetime John likes to go hiking and bicycling.
Probability Calculator English
Published: Sun Jan 08 2023
In category Mathematical calculators
Add Probability Calculator to your own website